A Basic Grid Object

What’s the point of formalizing something so basic? Judicious laziness, as always. Anything that makes for less typing and/or less thinking is a bonus in my world. Here’s a grid and some accessories that help on both fronts.

The Overload2D protocol

Overload2D is a set of arithmetic operations on ordered pairs, for example, CGPoint. With Overload2D you can add and subtract a CGPoint to another (or CGSize or CGVector, or indeed, any ordered pair that conforms to the Overload2D protocol). You can multiply and divide by scalars or by ordered pairs. There are various utility functions and variables available, such as hypoteneuse and area for size-like pairs, and (r, θ) representation for vector- and point-like pairs.

KGPoint, KGSize, KGVector

Basic ordered pairs: (x, y), (width, height), and (dx, dy), respectively. Analagous to Swift’s CGPoint/Size/Vector, but with Int rather than CGFloat as the data type for the pair elements. This results in each cell having a unique, whole-number address that will never be affected by rounding when used in calculations. These all conform to Overload2D, of course.

Sensor Rings

In the handful of “Snake” AI genetic algorithm implementations I’ve looked at, the snake can “sense” only the cells adjacent to its head. In Arkonia, my gremlins’ sensory ranges vary based on genetics and health.

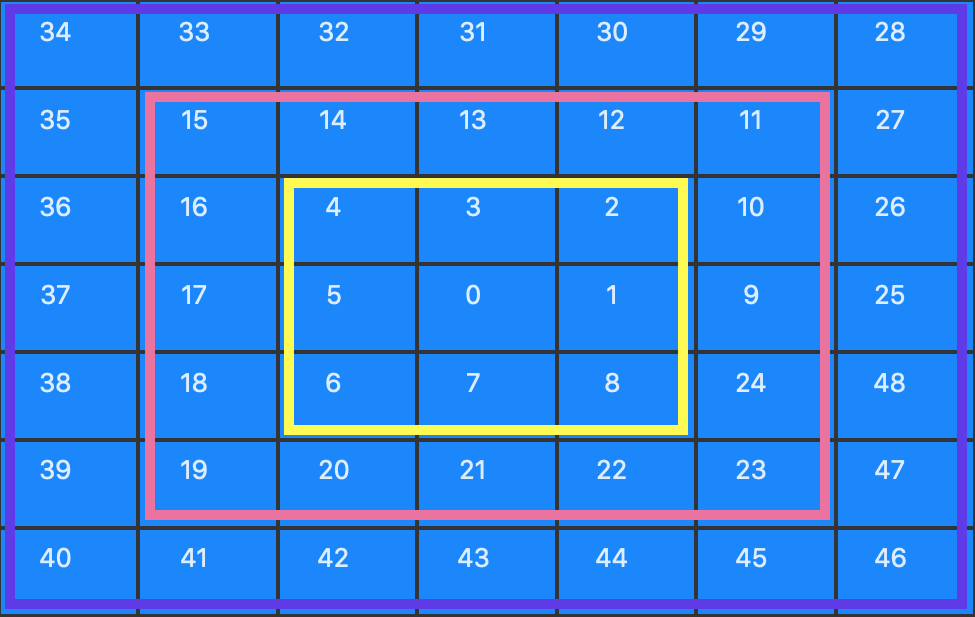In the upper diagram, consider a snake with its head sitting in the center, at the cell marked ‘0’. The usual snake’s sensor range is one “ring” – it reaches out to all the adjacent cells, 1-9 (actually, it seems that most of the snakes can see only three adjacent cells; an evolutionary dead-end if I ever saw one). This grid implementation enables linear iteration through the surrounding cells in these squarish “sensor rings”.

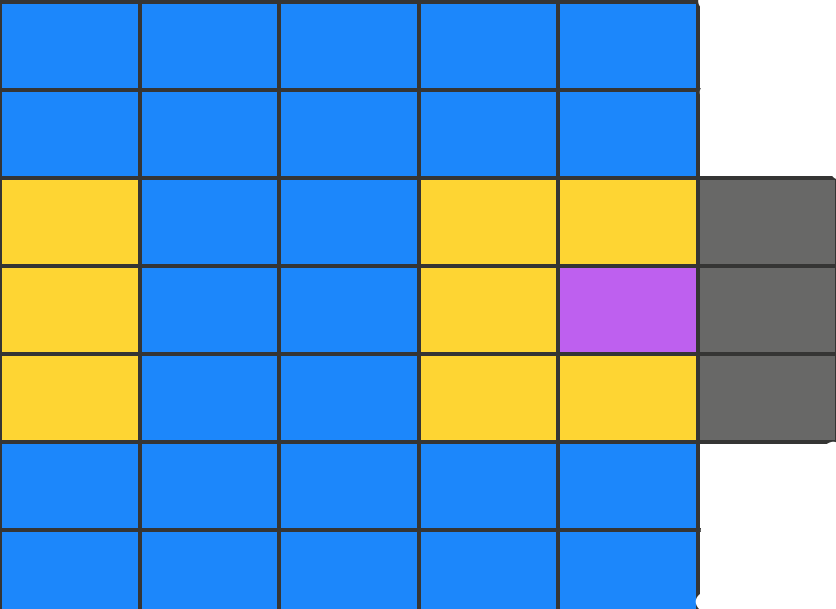
Asteroidization

Each element in the sense ring contains two important landmarks:

  • The real grid position, representing the wrap-around point where you need to put your gremlin if your world is a wrap-around world.
  • The virtual grid position, representing a point off the grid where the gremlin would go if it were to continue beyond the boundary without wrapping.

The primary purpose of the virtual position is to allow your game to determine the distance the gremlin will be moving, in case there’s a cost for moving, for example. In the lower diagram, consider the purple cell to be where the gremlin is currently sitting. When requesting cells by sense ring, you will get back the real positions as shown here in yellow, and the virtual positions as shown in gray.

Of course in most of the Snake AI implementations I’ve seen, the edges are walls; there’s no warping across space, the snake just dies under the cruel talons of natural selection. Sadists and snake-haters need not worry; there is an isOnGrid() function for them.

The Details

Using Overload2D and KGPoint/Size/Vector

There aren’t any surprises here. You can add and subtract 2D objects, you can multiply and divide 2D objects with scalars. Size objects have an area variable, vectors have an analagous magnitude variable. Have a quick scan of Overload2D.swift to see what’s available.

Asteroidization

struct AsteroidPoint {
  let realCell: GridCell
  let relativeVirtualPosition: KGPoint
}

For use with sensory functions, ie, functions that read cell contents via an index relative to a center

  • Properties:
    • realCell: the cell at the real grid location corresponding to the center+localIx. This is where you will want to place your gremlin to make it wrap to the other edge of the grid
    • relativeVirtualPosition: a position (not a cell) that’s not on the grid, where the gremlin would go if the grid were actually to extend far enough

Cell Addressing Functions

cellAt(_ position: KGPoint) -> GridCell

Gets the cell at the indicated absolute position on the grid

Parameter: position

The cell’s position on the grid. The point (0, 0) is in the center of the grid, with y increasing upward and x increasing to the right

Returns:

The indicated cell

cellAt(_ localIndex: Int, from center: KGPoint) -> GridCell

Gets the cell at the “ring index” relative to the indicated cell

Parameters:
  • localIx: The index to offset from the center
  • center: The cell to use as the center; a typical use for this function is to enable your game gremlin to read information (“sensory” input) in the surrounding cells, out to any arbitrary distance
Returns:

The indicated cell

first(fromCenterAt centerCell: GridCell, cMaxCells: Int, where predicate: @escaping (AsteroidPoint) -> Bool) -> AsteroidPoint?

Find the first cell from among the cells surrounding the center that results in predicate(_: AsteroidPoint) returning true

Parameters:
  • centerCell: The cell from which to offset
  • cMaxCells: The maximum number of cells to read for the search
  • predicate: Your function for testing the characteristics of candidate cells.

Returns:

The first qualifying cell – nil if no qualifying cell is found

Miscellany

isOnGrid(_ position: KGPoint) -> Bool

Indicates whether the specified position is on the grid.

makeIterator() -> IndexingIterator<[GridCell]>

For iterating over all the cells in the grid Note: Although the index is an Int, don’t try to use it for calculating offsets or positions of cells. Instead, if you need to know the position of a cell, grab the cell using the iterator then get cell.properties.gridPosition